Decibels are units so common for anything related to sound or music. By themselves, they have very little meaning—the suffixes give it context—wait, what? Let’s get rid of the confusion once and for all!

Ring, Ring! This is Alexander Bell calling

The Bel is a logarithmic unit, named after Alexander Bell (the guy who invented the telephone). In 1923 it replaced the mile of standard cable unit, which—at the time—was used to describe power ratio between two points on a telephone cable. The Bel is not exactly the same, as the unit is frequency-independent (the m.s.c. was only concerned with an 800Hz signal). More importantly, the Bel is a metric unit, so any metric prefix will apply. That said, in practical terms, only the decibel (=one-tenth of a Bel) is really used in the audio/sound/acoustics world.

Some logarithm background info

It’s easier to look at the decibel as a concept, not something inherently related to anything specific. It’s merely a logarithmic ratio between two given numbers—one of these usually a reference value. A logarithm is simply an exponent ({a^y} = x ) in a different order:

log_{a}(x) = y

• log_{a} is the base
• (x) is the argument
• Note: The decibel uses the common log, which has a base of 10 (log_{10})

To express a change of power in Bels:

log\left(\frac{P_{1}}{P_{0}}\right)

• P_{0} is the reference/starting power
• P_{1} is the new power value we’re comparing to the reference value

We know the Bel unit is a metric unit, therefor, the decibel is a tenth smaller. To express a change of power in decibels, we simply multiply the equation by 10:

10log\left(\frac{P_{1}}{P_{0}}\right)

Why use logarithms?

Our ear does not respond equally to equal changes in power, but rather to equal changes in power ratios (read more about how our hearing works). We would not experience an increase from 20W to 30W to be just as big as an increase of 10W to 20W. (20W ->40W would be).

10log\left(\frac{20}{10}\right)=3.01dB    |    10log\left(\frac{40}{20}\right)=3.01dB

As shown above, a doubling of power represents a +3dB increase. So regardless whether the increase is from 10W-20W, or from 575W-1150W, the logarithmic increase is identical, and thus +3dB.

Additionally, logarithms are used to reduce huge ranges of numbers down to more manageable ranges. For instance, the threshold of hearing lies somewhere around 20µPa (20 micro pascals) for most people; the point where experiencing sound begins to physically be painful is at ~20Pa. This is an awkward range to be expressing amplitude levels in. (In fact, the same auditory range in sound power ranges from 0.000000000001W to almost 100W—talk about quite the range!) Naturally, a range such as 0–120 would be a lot simpler, agreed?

It’s the suffixes that tell the story

So, how did we get to the range above (0–120)? Expressing numbers without context in decibels is pretty meaningless. It’s really the suffixes that give context and meaning to decibel values. Some decibel suffixes you’ll absolutely come across in the audio industry:

Suffix	Note
dBA	Depicts an SPL value as measured by an A-weighted SPL meter
dBC	Depicts an SPL value as measured by a C-weighted SPL meter
dB SPL	Sound Pressure Level. 0dB SPL = 0.00002Pa (20µPa)
dBu	0 dBu = 775 mV (milliVolt)
dBV	0 dBV = 1 V (Volt)
dBm	0 dBm = 1 mW (milliWatt)
dBW	0 dBm = 1 W (Watt)

When dealing with specific acoustics-related things, you’ll often come across dB SIL and SWL numbers as well, both dealing with the intrinsic acoustic intensity/power emittance properties of the sound source. The suffixes related to voltages and wattages you’ll come across when dealing with audio gear and speakers. For the remainder of this article, we’ll only be concerned with Sound Pressure Level (SPL).

Decibels and sound pressure

There is really no way for us to measure power directly, we can only calculate power using other known values (such as voltage and impedance):

P = V^2 / I

Because acoustic intensity is proportional to the square of acoustic pressure, we get the following:

L_{p} = 10log\left(\frac{P^2_{1}}{P^2_{0}}\right)  \longrightarrow  L_{p} = 20log\left(\frac{P_{1}}{P_{0}}\right)

That said, we can definitely measure pressure (or voltage). For electricity, you’d use a multimeter; for sound, you would use an SPL meter. While knowing the acoustic power/intensity of a sound source can be important in some scenarios, the majority of the time, knowing the sound pressure (L_{p}) will be sufficient enough to tell the entire story. Additionally, more people will be able to ‘grasp’ the concept of sound pressure easier, rather than sound power.

A doubling of the sound pressure will now yield (because of the 20*log, instead of 10*log) an increase of +6dB:

L_{p} = 20log\left(\frac{2}{1}\right)=6.02dB SPL

In other words, making a sound pressure twice as loud, will yield in an SPL increase of +6dB.

Note that the 0.02 is usually omitted because in most cases it’s usually too insignificant to be relevant. This all said, our hearing doesn’t necessarily follow black-and-white rules of math and therefore the average ear will experience an increase of ~10 dB SPL as being twice as loud. The more the ears are ‘trained’ (as with musicians, producers, and engineers), the more this number gets closer to 6dB SPL.

So when you measure an SPL of 94dB and make the sound source twice as loud and perform an amplitude measurement, you will read an amplitude level of 100dB SPL (an increase of +6dB).

Extended exposure to sound pressure levels

In the US, the Occupational Safety and Health Administration (OSHA) is responsible for settings legal limits on workplace noise exposure. Their limits (1910.95(b)(2)) list the following:

dBA	Max. exposure time
85	16 hours
90	8 hours
92	6 hours
95	4 hours
97	3 hours
100	2 hours
102	1.5 hours
105	1 hour
110	30 minutes
115	15 minutes or less

To give you some context and reference in terms of amplitude levels:

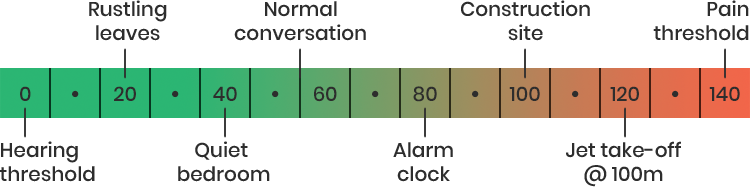
The National Institute for Occupational Safety and Health (NIOSH) is the federal agency responsible for doing research and making recommendations regarding workplace injury prevention. While the OSHA’s standards above show the current legal limits, the NIOSH has actually made changes to the above numbers:

dBA	Max. exposure time
82	16 hours
85	8 hours
88	4 hours
91	2 hours
94	1 hour
97	30 minutes
100	15 minutes
103	7 minutes 30 seconds
106	3 minutes 45 seconds
109	1 minute 52 seconds
112	56 seconds
115	28 seconds
118	14 seconds

The new levels follow a 3dB exchange rate, with 85dBA at 8 hours being the starting point (every 3dB increase cuts the recommended max. exposure time in half). If we would compare the recommended maximum exposure time for a sound level of ~94dB SPL, the OSHA regulation recommends 4 hours without causing permanent damage, the NIOSH recommendation recommends a maximum of 1 hour; indeed quite the discrepancy. After years of data collection on this subject, it appeared 20% of people still suffered some hearing loss while abiding by the OSHA recommendations; perhaps it is time to revisit this regulation.

Take care of your ears—you only get one set. Do your mixing at a sensible listening level, and you’ll be able to trust your hearing for a long time.